다층 퍼셉트론
1. 여러 개의 퍼셉트론을 결합한 다층 구조를 이용하여 선형 분리가 불가능한 상황을 해결함
은닉층을 둠
-> 은닉층은 원래 특징 공간을 분류하는 데 훨씬 유리한 새로운 특징 공간으로 변환함
시그모이드 활성함수 도입
-> 퍼셉트론은 계단함수, 다층 퍼셉트론은 로지스틱 시그모이드나 하이퍼볼릭 탄젠트 사용, 딥러닝은 소프트플러스나 렉티파이어에 주로 사용됨(기울기 소멸 방지)
오류 역전파 알고리즘 사용
-> 여러 층이 순차적으로 이어진 구조라서 역방향으로 진행하면서 한 번에 한 층씩 그래디언트를 계산하고 가중치를 갱신함
2. 인식
신경망은 학습을 마치면 훈련집합 대신 가중치만을 저장함
3. 특성
- 오류 역전파 알고리즘의 빠른 속도
- 모든 함수를 정확하게 근사할 수 있는 능력
- 성능 향상을 위한 휴리스틱의 중요성
은닉층
- 은닉층은 원래 특징 공간을 새로운 특징 공간으로 변환하는 feature extractor라고 볼 수 있음
- 새로운 특징 공간은 다층 퍼셉트론이 목적을 달성하는 데 더 유리해야함
- 예전에는 사람이 고안한 특징 추출기로 특징 벡터 추출 후 은닉층 1~2개가 추가로 특징 공간을 변환하는 접근 방법을 주로 사용함
--> hand-crafted featrues : 사람이 고안한 특징
- 딥러닝에서는 센서로 획득한 원시 신호를 입력받아 여러 단계의 은닉층이 자동으로 계층적인 특징을 추출하는 접근 방법을 사용함
--> 은닉층들이 추출한 low-level feature를 뒤 쪽의 은닉층이 입력받아 추상화된 high-level feature를 추출함
오류 역전파 알고리즘
여러 개의 퍼셉트론을 결합한 다층 구조를 이용하여 선형 분리가 불가능한 상황을 해결함
목적함수(비용함수)
- 기계학습은 X를 완벽하게 Y로 매핑하는 최적의 함수 f를 알아내야 함
- 현실과 타협하여 근사 최적해를 구함.
- 기계 학습은 다층 퍼셉트론의 출력과 주어진 부류 정보 Y의 차이를 최소로 하는 최적의 매개변수를 찾아내야 함
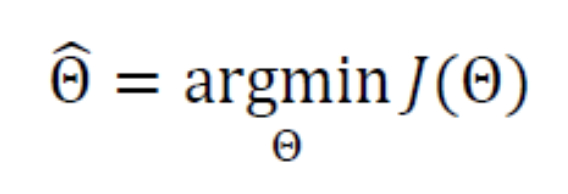
오류 역전파 알고리즘
오류를 전파할 때 쓸 그래이디언트값을 구하는 방법을 지칭함
미니배치 스토캐스틱 경사 하강법
스토캐스틱
- 오류 역전파를 이용해서 한 샘플의 그래디언트를 계산한 후 다음 가중치를 즉시 갱신함 -> 모든 샘플에 수행하면 한 에포크가 지나감
- 한 샘플로 계산한 기울기는 잡음을 많이 포함해서 최저점을 찾아가는 경로가 매개변수 공간에서 갈팡질팡하는 경향을 보임
- 수렴 시까지 많은 시간이 걸림
배치 방식
- 모든 샘플의 기울기 계산 후 평균 그래디언트를 구해서 한꺼번에 갱신함
미니배치
- t를 수십~수백의 크기로 설정해둠
- 훈련 집합 X에서 t개의 샘플을 무작위로 뽑아 미니배치를 구성하고, 미니배치에 속한 샘플의 그래디언트 평균으로 가중치를 갱신
- 수렴 속도와 GPU를 사용한 병렬 처리에도 유리함
- 미니 배치를 무작위로 뽑아서 학습 완료시까지 한 번도 학습에 참여하지 않는 샘플이 존재할 수 있음
- 미니배치는 모든 샘플의 대략적인 대표성을 띠므로 성능에 해를 끼치지는 않음
- 훈련 집합을 모두 사용하기 위해서는 훈련집합의 순서를 충분히 섞은 후, 미니배치 단위로 나누고 미니배치를 순서대로 처리하면 됨
- 높은 랜덤으로 일종의 규제 효과를 가져다 주고 일반화 능력이 향상됨
- 딥러닝 등에서는 미니배치를 표준으로 사용하게 됨.
'ML' 카테고리의 다른 글
| 생성 모델 (0) | 2023.01.11 |
|---|---|
| CNN (0) | 2023.01.10 |
| Deep Learning (0) | 2023.01.03 |
| 기계 학습과 수학 (0) | 2023.01.02 |
| Machine Learning (1) | 2023.01.02 |